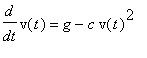Maple Tool1.mws

Maple Tool 1

This worksheet illustrates the process described in Section 5.2 for obtaining an approximate solution of the initial value problem

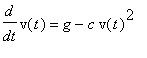diff(v(t),t) = g-c*v(t)^2   with   v(0) = 0 .

>    with(plots):with(DEtools):

For drops of diameter 0.05 inches or approximately 0.004 feet, the value of c  is.

>   

>    c:=0.115;

We enter a value for g  in feet per second squared:

>    g:=32.2;

We consider the velocity of the drop for the first two seconds. The time step Delta = Delta*t  is determined by the number of divisions n  of the 2-second time interval.

>    Delta:=2/n;

>    t:=k->k*Delta;

We plot the approximate solution together with the slope field for the differential equation.

>    DE:=diff(v(t),t)=g-c*v(t)^2;
sfield:=dfieldplot(DE,[v(t)], t=0..2, v=0..25):%;

We do the first two steps in the approximation individually.

>    n:=10;
v[0]:=0;
v[1]:=(g-c*v[0]^2)*Delta;

>    v[2]:=v[1]+(g-c*v[1]^2)*Delta;

Now we calculate the all the steps.

>    n:=10;
Delta:=2/n;
v := proc(k)

>         v(k) := v(k-1)+(g-c*v(k-1)^2)*Delta;

>    end:                                                  

>    v(0):= 0:

Check the values for v[1]  and v[2] .

>    v(1);
v(2);

Plot the approximate solution for n  steps.

>    solution:=[seq([t(k),v(k)],k=0..n)]:
solPlot := plot(solution, t=0..2, v=0..25, style=POINT,symbol=circle, color=blue, thickness=2): %;

We compare this approximate solution with the slope field.

>    display(sfield,solPlot);

We also compare the approximate solution to the symbolic solution stated in Section 5.1.

>    V:=t->sqrt(g/c)*(1-exp(-2*sqrt(g*c)*t))/(1+exp(-2*sqrt(g*c)*t));

Start with n = 10  and then double the number n  of calculation steps. (The following block of commands repeats all the essentials from above.)

>    n:=10;
Delta:=2/n;
v := proc(k)

>         v(k) := v(k-1)+(g-c*v(k-1)^2)*Delta;

>    end:                                                  

>    v(0):= 0:
solution:=[seq([t(k),v(k)],k=0..n)]:

solPlot := plot(solution, t=0..2, v=0..25, style=POINT,symbol=circle, color=blue):

>    Vplot:=plot(V(t),t=0..2, color=green,thickness=2):
display(Vplot, solPlot);

Go back to the most recent definition of n , and double twice more, comparing the symbolic and numerical solutions each time you double the number of calculation steps.

>